We Hope You've Conserved Your Energy for This Section

The First Law of Thermodynamics

Thermodynamics. The mere word strikes fear in the hearts of almost all who hear it. Or see it. There's nothing to fear, though. Shmoop is here.

Step 1: Break thermodynamics down. "Thermo" = heat. "Dynamics" = change. Thermodynamics examines how energy and heat are related.

Step 2: Figure out this "First Law" thing.

Step 3: Get a sandwich.

Back to step 2. The first law of thermodynamics is a lot like the law of conservation of energy. Energy can be neither created nor destroyed. It can change forms, though.

The first law of thermodynamics looks at the energy of a chemical system. This can be a tiny solution, a large pot of spaghetti, the sun, or anything else where a chemical or physical process can occur. This system has energy in it. The molecules have bonds that have chemical energy in them. The molecules are moving, giving them thermal energy. The total of all of the energy in the system is its internal energy (U). In system = internal energy. Easy peasy.

The amount of energy in a system depends. Depends on what, you ask? On several things:

• Temperature
• Pressure
• Concentration/Quantity of stuff
• Phase of matter
• How spicy its burrito is

Okay, that last one isn't true, but the others are. Change one or more of them, and our internal energy changes.

The change in the internal energy (ΔU) can be accounted for. After all, energy can't disappear. It can go into one of two directions.

• Heat (q)
• Work (w)

Heat is the thermal energy in a system. More heat = faster movement of atoms and/or molecules. Heat moves from one system to another, from areas of high heat to areas of low heat. This explains why we want to sit by the fire when our fingers are frozen from throwing snowballs or why want to go swimming in a cool pool during a hot summer day.

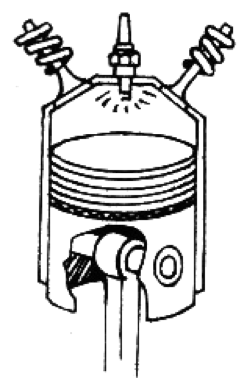
When we say the word "work" in thermodynamics, we don't mean waiting tables at Pizza Hut. Work is defined as moving an object with a given force (F) through a distance (d). This is typically done by gas systems, which can expand or contract more easily.We can calculate the work done in a gas system. Think about an engine piston. The reaction occurs in a small volume with the piston pressing down with a given pressure. The reaction causes the volume to expand. This reaction is doing work, and the formula is w = -PΔV.

We can also describe the first law with a mathematical equation: ΔU = q + w.

Put the two reactions together and you get this: ΔU = q – PΔV.

If we're more interested in the heat, we rearrange this to get q = ΔU + PΔV.

At a constant pressure, we have q_p = ΔH = ΔU + PΔV.

ΔH is the change in enthalpy. Enthalpy is also described as the heat of reaction (at constant pressure). Does your reaction cause the reaction vessel to get warm to the touch? Then the reaction is exothermic (gives off heat; ΔH is negative). If the reaction vessel feels cold, then the reaction is endothermic (absorbs heat; ΔH is positive).

You might be thinking, "Wait just a gol-danged minute here. Shouldn't a positive ΔH mean that stuff is getting hotter, and a negative ΔH means things are getting colder?" Remember, though, that we're describing the heat within the system. If ΔH is negative, that means the system is losing heat—and giving it off to anything that's nearby. Like, say, our hands on a toasty mug of hot cocoa.

The Second Law of Thermodynamics

Have you ever wondered why bedrooms never seem to stay clean? We pick up our clothes, run the vacuum, even dust, and two days later it looks like a mini tornado passed through. What happened?

The answer is the second law of thermodynamics. It's our go-to excuse whenever someone yells at us about cleaning our room, but let's focus on the chemistry.

The second law of thermodynamics states that randomness happens spontaneously. On the flip side, it takes energy to create order. Scientists have come up with a term for disorder: entropy.

Another way of putting the second law of thermodynamics states that whenever something spontaneous happens within a system, the entropy of the system and its surroundings must increase. In other words spontaneity leads to disorder.

Entropy is symbolized with the variable S. Just think "spontaneous" to remember that entropy = S.

Entropy is interesting in and of itself, but we're generally more interested in the change in entropy (ΔS). Going back to the bedroom metaphor, chemists are mostly interested in knowing whether energy has been put into the room to make it tidy or whether the change has been for the worse.

One last thing we should point out: entropy increases with increased freedom of movement of a person, place, or thing, and heck even places. That means that, for the various states of matter, entropy increases in the order of solids < liquids < gases < plasma.

Third Law of Thermodynamics

The third law of thermodynamics runs a bit under the radar. The first law has enthalpy and the second law has entropy. What does the third law have? Alas, no cool variables. It's the uncool younger sibling who tags along.

The third law basically covers what happens when something reaches 0 Kelvin. What would such an exotic substance look like? The third law states that we'll have a perfect crystal at 0 Kelvin, and that it will have zero entropy. This makes perfect sense. A perfect crystal is perfectly ordered. At absolute zero, there is no thermal motion. Perfectly ordered solid + no thermal motion = zero entropy.

Does this situation ever happen in real life? Not that we've been able to verify. To start with, perfect crystals are exceedingly difficult to create, if not impossible. In addition, no scientist has ever been able to achieve absolute zero. Scientists have gotten extremely close to achieving absolute zero, though, and if nothing else, the third law of thermodynamics does give us a finite end point when it comes to entropy.

Gibbs Free Energy

The best things in life are free. Right? Who doesn't love presents? In chemistry, even energy can be free. Okay, not exactly. Gibbs Free Energy (G) is free in the sense that it's the amount of energy that's available to do work. It ties enthalpy, entropy, and temperature together with a nice mathematical bow.

ΔG = ΔH – TΔS

Gibbs free energy is extremely useful to scientists to describe a reaction.

• If ΔG < 0, then the reaction is spontaneous
• If ΔG > 0, then the reaction is not spontaneous
• If ΔG = 0, then the reaction is at equilibrium

Sometimes you see this equation written like this: ΔG&deg; = ΔH&deg; – TΔS&deg;

Those are not degree signs or halos near the letters. While we love this equation, the variables are not blessed in any way. The halos indicate that the reaction is being performed at standard state conditions, which are listed below.

• 1 molar solutions
• 298 K
• 1 atm pressure

Why do we care about "standard state" conditions? What if we want to run a reaction at different conditions? While wearing our pajamas?

Simply put, standard conditions give chemists a common set of ground rules to work with so everyone can compare data. Thanks to having standards, all sorts of information about enthalpy, entropy, and free energy of formations at standard conditions is readily available. We can use this to determine the enthalpy, entropy, and free energy for a reaction at standard conditions.

More good news. If we assume that ΔH&deg; and ΔS&deg; do not change with temperature, then we can find ΔG&deg; at any temperature.

Some reactions prefer the cold. Some reactions prefer the heat. Some reactions happen no matter what. Others will never happen, like, ever.

This table helps to summarize things.

ΔH△	ΔSΔ	Spontaneous at Low Temps	Spontaneous at High Temps
< 0	< 0	Yes	No
< 0	>0	Yes	Yes
>0	>0	No	Yes
>0	<0	No	No

Brain Snack

Keeping track of changes doesn't always have to hurt our brains, particularly when it comes to puppies.