The coordinate plane is split into four sections or quadrants, like so.
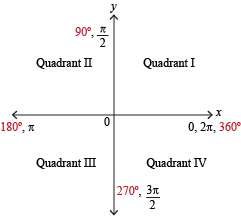
Notice how 90° is right there at the positive y-axis. That's because 90° is exactly one-quarter of a full circle. We can also see that 180° sits right between Quadrant II and Quadrant III, and 270° separates Quadrant III and Quadrant IV.
Acute angles (that is, smaller than 90°…and adorable) fall into Quadrant I. Angles larger than 90° fall into one of the other three quadrants. To simplify trigonometric expressions, we often rewrite non-acute angles as acute angles. To do this, we first need to learn all about reference angles.
Reference Angles
A reference angle is just the acute version of whatever angle we're looking at. It's the smallest angle that our angle makes with the x-axis. Let's use a ρ to represent our reference angles, which is just the common Greek letter "rho." As in, "Rho, rho, rho your boat."
Since we're on a Greek fix, we'll use ɵ ("theta") to represent the actual angle.
First, let's look at Quadrant I.

No need for anything fancy in Quadrant I. Our reference angle is ρ = ɵ, because it's already an acute angle.
On to Quadrant II. This one is a little trickier.

In Quadrant II, ρ = 180° – ɵ or ρ = π – ɵ. In other words, to turn ɵ into ρ, we subtract ɵ from 180° (or from π radians if we're in radian mode).
Now, Quadrant III.

In this quadrant, ρ = ɵ – 180° or ρ = ɵ – π.
Finally, Quadrant IV.
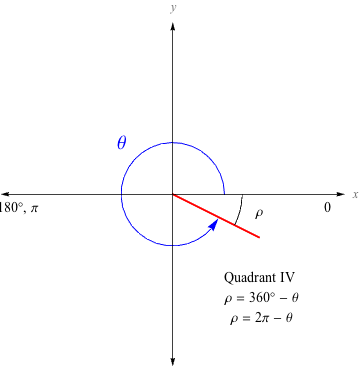
In Quadrant IV, ρ = 360° – ɵ or ρ = 2π – ɵ.
One little thing, though: our ɵ has some special requirements. It's gotta be within one full circle.
0° ≤ ɵ ≤ 360° or 0 ≤ ɵ ≤ 2π
If ɵ doesn't fall into this range, then we must add or subtract 360° or 2π, until we have a ɵ in the correct range.
Now let's look at our six trig functions and see what their signs are for each quadrant.

In Quadrant I, all six trig functions are positive.
In Quadrant II, only sine and its reciprocal function cosecant are +. The other four trig functions are negative.
In Quadrant III, only tangent and its reciprocal function cotangent are +.
In Quadrant IV, only cosine and its reciprocal function secant are +.
An easy way to remember this is ASTC (All, Sine, Tangent, Cosine), or All Students Take Calculus.
Calm down; it's just a mnemonic device. And no, you don't have to take calculus—yet.
Now, let's see what we can do with our newfound knowledge.
Sample Problem
Find the reference angle for 135°.
First off, we need to figure out which quadrant we're in. Since 135° is more than 90° but less than 180°, our angle is in Quadrant II.

That's 135° measured from the positive x-axis. We wanna turn that into an acute angle that's closer to the negative x-axis, because that angle will be smaller and easier to deal with.
In Quadrant II, our formula is ρ = 180° – ɵ. Plug in ɵ = 135°.
ρ = 180° – 135°
ρ = 45°
Sample Problem
Find the reference angle for 330°.

We've got an angle that's between 270° and a full 360°, so we're in Quadrant IV this time. Our formula is ρ = 360° – ɵ.
ρ = 360° – 330°
ρ = 30°
Sample Problem
Find the reference angle for 480°.
Uh-oh...480° doesn't fall into our 0° ≤ ɵ ≤ 360° range.
Since 480° is larger than 360°, we've gotta subtract 360° to get our ɵ.
480° – 360° = 120°

Much better: 120° falls into Quadrant II.
In Quadrant II, ρ = 180° – ɵ. Plug and chug.
ρ = 180° – 120°
ρ = 60°