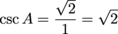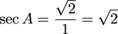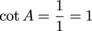We've covered sine, cosine, and tangent. We're experts on one little piece of trigonometric real estate. (Marvin Gardens? Park Place? Boardwalk? Pull out your Monopoly money.) Kudos to you, but there's more.
Sine, cosine, and tangent each have a reciprocal function. Reciprocal, reciprocity—think of flipping things over, like hamburgers on a grill, pancakes on a griddle, eggs over easy. (When do we eat?) We already know that regular numbers have reciprocals (2 and 1/2 are reciprocals, for example), but we can also flip our trig functions on their heads.
Cosecant is the reciprocal of sine. Its abbreviation is csc. To determine csc, just flip sin over.
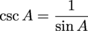
Secant is the reciprocal of cosine. Its abbreviation is sec. To determine sec, just flip cos over.
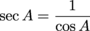
Cotangent is the reciprocal of tangent. Its abbreviation is cot. To determine cot, just flip tan over. (Try remembering it all by thinking, "After an evening of sin, Joe stretches out on a cot in the backyard and later flips over to get a better tan." Weird, but it works.)
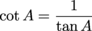
And no, they don't sizzle when they're flipped.
Sample Problem
If a = 8 and b = 15, find the six trig ratios of angle A.

We're gonna need that missing hypotenuse, so first use a2 + b2 = c2 to find c.
82 + 152 = c2
64 + 225 = c2
289 = c2
c = 17
Now let's plug those sides into our relationships for sin, cos, and tan. Remember SOHCAHTOA. We're looking at angle A, so the opposite side is 8, the adjacent side is 15, and the hypotenuse is 17. Ready, go.
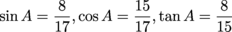
Now we take the reciprocals, or flip each function over.
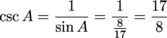
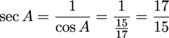

Sample Problem
What are the six trig ratios of angle B?
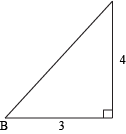
Once again, we'll need to track down that hypotenuse before we can take a trip to TrigVille. Give your buddy Pythagoras a call.
a2 + b2 = c2
We know the two legs of the triangle, so plug 'em in for a and b.
32 + 42 = c2
9 + 16 = c2
25 = c2

c = 5
Next, find the sine, cosine, and tangent of angle B.

To find the reciprocals, just flip the fractions over.
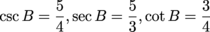
Sample Problem
An isosceles right triangle has two legs with a length of 1. If angle A is one of the non-right angles, what are the sine, cosine, tangent, cosecant, secant, and cotangent of angle A?
"Isosceles" looks pretty weird, but it really just means both legs have the exact same length. We don't have a picture to help us out, but who needs pictures? We're math detectives up in here.
All right, so we know both legs, which means a = 1 and b = 1 in our Pythagorean Theorem. Let's find c.
12 + 12 = c2
1 + 1 = c2
c2 = 2
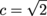
There's our hypotenuse. Now, we know angle A is not the triangle's right angle. It's one of the other guys, which means its opposite side and adjacent side are both 1. Apply the trig ratios, and don't forget to rationalize your denominators.

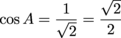

When flipping over your fractions to find the reciprocals, use the original fraction (with the pre-rationalized denominator). It will save you time and heartache.