Let's take all this highfalutin knowledge and use it in some real, live problems. Otherwise, it's just hanging out at the mall all day spending money on handbags.
Sample Problem
Find  .
.
First, we need to ask ourselves: where is cosine positive? (Is it near Waldo?)

Cosine is positive in Quadrants I and IV, but inverse cosine is limited to the range [0, π], so we're in Quadrant I.
Now we ask ourselves: for what angle is  ?
?
Knowing your reference triangles will be really helpful here (along with an extra-large pizza, hold the anchovies).


Sample Problem
Find  .
.
Where is sine positive?

Sine is positive in Quadrants I and II, but inverse sine is limited by  . Therefore, we must be partying in Quadrant I. We ask ourselves: for what angle is
. Therefore, we must be partying in Quadrant I. We ask ourselves: for what angle is  ?
?
Think: reference triangles.


Sample Problem
Find tan-1(1).
Where is tangent positive?
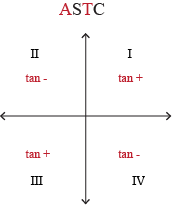
Tangent is positive in Quadrants I and III, but inverse tangent is limited to the range  . That's just how he rolls. We must be in Quadrant I.
. That's just how he rolls. We must be in Quadrant I.
Again, we ask ourselves: for what angle is tan θ = 1?
Reference triangles, anyone?

tan-1(1) = 45°
Sample Problem
Find  .
.
Ask yourself: where is cosine negative? (That's so rad...)

Cosine is negative in Quadrants II and III, but inverse cosine is limited to [0, π]. So our angle's gotta be in Quadrant II.
We ask ourselves: for what angle is  ? Man, we're sure asking ourselves a lot of questions.
? Man, we're sure asking ourselves a lot of questions.
Think: reference triangles (if you're tired of thinking, chill with "Angry Birds").


If you're stuck on the 150°, here's what you can do. The reference angle is 30°, but we're in Quadrant II right now. That means we need to subtract our reference angle from 180° to get the actual angle.
180° – 30° = 150°
Sample Problem
Find 
Whoa. What we're really looking for is the tangent of the angle whose cosine is negative one-half. Let's work from the inside out. (This approach works in math, and maybe psychology.)
Solve the inside first. For what angle is  ?
?
Once again, it's back to those reference triangles, but now ask yourself that weighty question: where is cosine negative?

But inverse cosine is bounded by [0, π], which means our angle is in Quadrant II.


Now we find tan(120°).

Tangent is negative in Quadrant II, so we'll have a negative answer.

So  .
.