The three wise men of the unit circle are 
. They bring with them gifts of knowledge, good grades, and burritos. That's a sweet haul.
We want to know each angles' x and y coordinates on the unit circle. Why? We'll never teeeellll.*
Let's start off with the angle 
. It's a 45 degree angle in radian disguise. That mustache isn't fooling anyone, though.
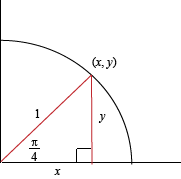
We can find x and y using the special right triangle for a 45 degree angle. The ratio of the sides is 
. In our case the hypotenuse is 1, so we need to solve 
. (A right triangle with side length s will be a 45-45-90 right triangle if the sides are length 
.)
Both sides are equal, so we have the point 
for the angle 
. We still won't tell why we want this information*, but we have it.
Now let's figure out the other two angles. 
is 30 degrees, while 
is 60 degrees. Yeah, the 3's and 6's not matching up can be confusing. We tried telling them that, but those wise-aleck angles told us, "Division does not work that way."
We can take care of both angles with one triangle. A 30-60-90 right triangle (or perhaps we should say a 
right triangle) has a ratio of 
, corresponding to the sides opposite 30:60:90. The hypotenuse is 1, so:
That gives us 
for , and 
for 
. Now we can talk about what all this stuff means.
You didn't think we'd really hold out on you? Pshaw.
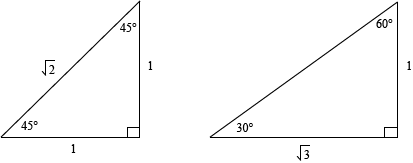
Take a look at the special right triangles. Notice anything interesting about them?
No, nothing? Can't say we blame you. How about you compare the sine and cosine of each angle to their points on the unit circle?
x = cos A
y = sin A
Can you feel your mind being blown? Cosine equals the x-coordinate for an angle, and sine equals its y-coordinate. By learning the points on the unit circle, we also learn sine and cosine for each angle.
That means we already know sine and cosine for 
and 2π. We're unlocking secret knowledge from our brains that we didn't know they had. Who knows what mutant power we'll develop next?
We'll be using all of these angles a lot from now on, so you definitely want to memorize their cosine and sine…or use this handy trick for keeping them straight. It's as easy as 1-2-3 1-2-3.
*We'll totally tell. Soon.