What is love? Well, we've heard that, when the moon hits your eye like a big pizza pie, that's amore, which is like love but foreign. If the moon were made entirely out of pizza, it probably wouldn't have taken people until 1969 to get there. There probably wouldn't be much moon left, either.
When it comes to pizza, we're a big fan of a good crust. We're such big fans that we started measuring the length of all our crusts (don't judge), and we figured something out.

If we cut a pizza in half, then each half has half of the total crust. If we cut it into fourths, then each slice has ¼ the crust. No duh, right? Well, this rabbit hole goes deeper. And it's full of pizza.
Sample Problem
A slice of pizza is cut with a 30° angle; the pizza has a 12 cm diameter. How many cm of crust is there?
Our first question is, what toppings are on this pizza? We're not eating any weird toppings, like caviar or pickles. Next we want to know how much crust is on the whole pizza. In math-speak, we're asking about a circle's circumference. That's C = 2πr, or 12π cm for our pizza.
Our last pizza puzzle piece is, how much of a pizza does 30° cover? Well, we can use change our angle into those new-fangled radians to figure that out. There are 360° in a circle, so it's:

That's not a lot. It's a mighty convenient number for us, though, because it means the length of our crust, what mathematicians would dryly refer to as the arc length, is π, or about 3.14, cm. Now that's what we call a pi crust.
In general, we can find the arc length by the formula  . We multiply the circumference of the circle by the fraction of the circle taken by the angle x. Things are even easier when we're working with radians. Then our formula is:
. We multiply the circumference of the circle by the fraction of the circle taken by the angle x. Things are even easier when we're working with radians. Then our formula is:
L = x r
We just multiply the angle by the radius (not the diameter) to get the arc length. If only we could find our socks this easily.
One last tidbit before we move on. Notice that, if the radius is 1, then the arc length equals the angle in radians. That means an angle in radians is the same as the arc length of that angle on the unit circle. Some people use this as an alternate definition for radians, and those people are math nerds.
More Pi-Filled Pies
The crust isn't the only good part of a pizza. We like the rest of it too, so now we're going to find how much of it we've got. That's like a thinly veiled excuse to do some math, and it sounds like finding the area of a circle.
Just like we took the circumference and chopped it up to find the arc length, we're doing the same with the total area to find the area of a sector. That's just some portion of a full circle.

When we're in degrees, we just multiply the total area by the fraction of the circle taken by our angle. When in Rome, do as the Romans do. And when we're in radians, well, let's replace that 360° with 2π and find out what happens:


We get rid of the π, we divide by 2, and we're done. Now that's a formula we can use.
Sample Problem
What is the area of a sector of a circle measuring 6 in across that has an angle of π?
We can just plug and chug into our formula.

Man, we are really hungry now for some reason. Maybe we'll order some Chinese food.
 We have a diameter of 10 cm, which means our radius is 5 cm. Plugging in our values, we get:
We have a diameter of 10 cm, which means our radius is 5 cm. Plugging in our values, we get:
 = 1.25π
= 1.25π
 in a circle with a radius of 5 units?
in a circle with a radius of 5 units?
 of the area. The total area is π(3)2 = 9π. so the area of the sector is 4.875π.
of the area. The total area is π(3)2 = 9π. so the area of the sector is 4.875π. in a circle with a diameter of 22 in?
in a circle with a diameter of 22 in? . The radius is 11 in, so:
. The radius is 11 in, so:

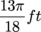
 in a circle with a radius of 12 mm?
in a circle with a radius of 12 mm?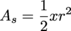

 in a circle with a diameter of 16 ft?
in a circle with a diameter of 16 ft?