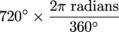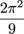The idea of using degrees to measure angles is somewhat arbitrary: the ancient Babylonians decreed that there were 360 degrees in a circle because it was convenient for them. Well, this isn't ancient Babylon, so that isn't good enough. We want to use a measure that's convenient for us.
It turns out that there is a more convenient measure to use for angles when working with trigonometry and calculus. The radian is a measure for angles based on the characteristics of circles. In particular, there are 2π radians in a full circle. Uh, 2π, 2π, where have we seen that before?
Why, the unit circle. (Bet you didn't see that one coming. No way, no how.)

The unit circle has radius 1, so its circumference is 2π.
Sample Problem
Convert the following from degrees to radians: 90°, 180°, 270°.
We want to be able to switch between radians and degrees like it ain't no thang. The secret to doing so is realizing that 360 degrees and 2π radians are equal. That means that:

But shhhh! Don't tell anyone. It's a secret.
From here, the problem is a straightforward case of unit conversion. We like straightforward.


An angle of  radians is the same as an angle of 90 degrees. This makes sense, because they are both
radians is the same as an angle of 90 degrees. This makes sense, because they are both  of the angle of a full circle. What does not make sense is an 8-foot tall Wookie living on the planet Endor. It does not make sense.
of the angle of a full circle. What does not make sense is an 8-foot tall Wookie living on the planet Endor. It does not make sense.


An angle of π radians goes halfway around the circle. There are not a lot of people we would go to the other side of a circle for, but pi is one of them. (Besides, pi owes us 20 bucks.)


The three angles we've looked at so far— , π, and
, π, and  —all fall on the axes of the graph. So do 0 and 2π. (They're even on the same one together: how scandalous.) These angles will act like reference points for us in later sections, to help us keep our bearing when working with unfamiliar angles.
—all fall on the axes of the graph. So do 0 and 2π. (They're even on the same one together: how scandalous.) These angles will act like reference points for us in later sections, to help us keep our bearing when working with unfamiliar angles.
They'll be like the constellations were for sailors in ancient times, but with less scurvy or getting lost because we actually aren't that good at sailing.
Sample Problem
Convert the following from radians into degrees:  , and
, and  .
.
Maybe we took things a little too fast. Let's see if we can go back to degrees from radians. Just in case this whole "working with radians" thing doesn't work out.


One down. The next one is:


We're knocking these out in double time.

Woah, wait up: angles can be greater than 360 degrees? What would that even look like?

Oh. It makes a full circle and then keeps on spinning. 420 degrees is actually the same as a (420 – 360) = 60 degree angle on the unit circle; it's also the same as  radians. When two angles have different measures but end up on the same spot on the unit circle, they're said to be coterminal.
radians. When two angles have different measures but end up on the same spot on the unit circle, they're said to be coterminal.
That makes it sound like both angles are dying together, but it really means that they terminate (that is, end) at the same place.
Anyway, it turns out that working with radians isn't that bad. We just have to relearn the sizes of some common angles;  is a right angle, 2π is a full circle, and so on. Once we do that, using radians is no harder than using degrees for angles.
is a right angle, 2π is a full circle, and so on. Once we do that, using radians is no harder than using degrees for angles.
All our fears were as unfounded as a twice-lost sock.
Get it? We found the sock once, but then we lost it again. We "unfound it." See, if you say it fast, it sounds like "unfounded." Th-that's funny, right? Okay, moving on.








 radians into degrees.
radians into degrees.

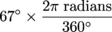
 radians
radians