ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
AP Physics 1 Videos 86 videos
AP Physics 1: 1.4 Waves. Which of the following is technically true for Max as he stands at the edge of oblivion?
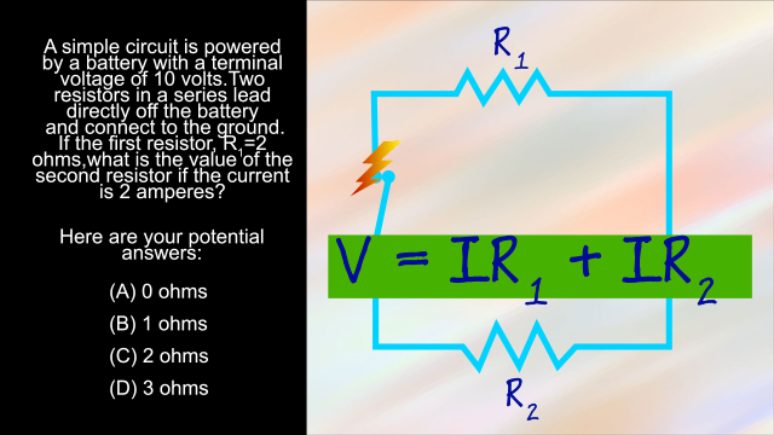
AP Physics 1: 1.4 Changes and Conservation Laws. Find the current across R2.
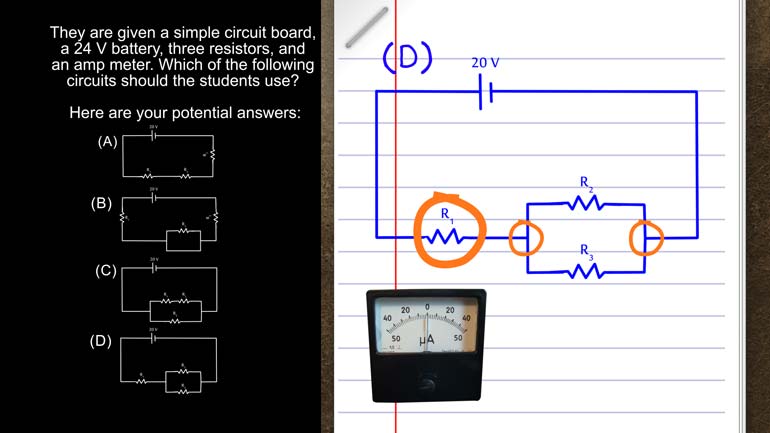
AP Physics 1: 2.4 Changes and Conservation Laws. Which of the following circuits should the students use?
AP Physics 1: 2.3 Changes and Conservation Laws 203 Views
Share It!
Description:
AP Physics 1: 2.3 Changes and Conservation Laws. Which of the following is closest to the maximum speed of the oscillating sphere?
More Video DetailsTranscript
- 00:00
Thank you We sneak and here's your smoke du jour
- 00:05
brought to you by springs it's Important understand how springs
- 00:08
work in terms of physics it's also important to understand
- 00:11
how springs work in terms of comedy Well a sphere
- 00:15
with a massive forty five kilograms hangs on a vertical
Full Transcript
- 00:17
spring With the spring constant k equals five thousand meters
- 00:22
at the bottom of its oscillations up announcing the sphere
- 00:26
barely touches the ground at the top It rises to
- 00:29
a height of three meters which of the following is
- 00:32
closest to the maximum speed of the oscillating sphere And
- 00:36
here the potential answers Anything that one all right well
- 00:41
before we really get into this don't get hung up
- 00:43
on the idea that this spring is hanging from the
- 00:45
ceiling What we did there don't get hung up on
- 00:48
never mind Anyway it affects the equilibrium point But for
- 00:51
this question that doesn't come into play With that out
- 00:56
of the way let's think about how the energy in
- 00:58
this system works Well when this spring is moving at
- 01:01
full speed all the energy and the system is kinetic
- 01:04
energy The equation for that is one half mass times
- 01:09
velocity squared Now at the moment of maximum displacement when
- 01:13
the sphere is that it's very highest and very lowest
- 01:17
point the sphere is actually not moving just for a
- 01:20
blink of an eye The energy is all stored his
- 01:22
potential energy Then the spring gets back to spring it
- 01:25
again and the kinetic energy comes back into play Going
- 01:28
going going So what That instant when the sphere isn't
- 01:31
moving all of the energy and the system is elastic
- 01:34
potential energy Well to calculate that we find the product
- 01:39
of one half the spring constant jonas k in our
- 01:43
little equation here times the amplitude squared Well that equation
- 01:47
looks like this and you stands in for elastic potential
- 01:50
energy Because it's just easier to type you know and
- 01:53
amplitude is the maximum displacement from the equilibrium point of
- 01:57
the spring In this case since the bottom of the
- 02:00
oscillation around level and the top of the oscillation is
- 02:03
three meters Will The amplitude is half of that or
- 02:06
one point five meters using advanced calculus Now we know
- 02:09
that in a system mechanical energy equals potential energy plus
- 02:13
kinetic energy And we also know that the total energy
- 02:17
in this system can't change unless something else acts on
- 02:20
it So the mechanical energy when all the energy is
- 02:23
potential is the same as when all of the energy
- 02:26
is kinetic Or to put it another way the maximum
- 02:30
kinetic energy of this system is equal to its maximum
- 02:33
potential energy Got it good And that means that the
- 02:38
two equations we looked at earlier have to equal each
- 02:40
other So you sometimes all this physics makes us feel
- 02:44
like our head is on a spring Now we can
- 02:46
plug in numbers and sol for velocity after we do
- 02:50
a little bit algebra With that we see that velocity
- 02:53
equals amplitude times the square root of a spring constant
- 02:57
over mass that's one point five meters times the square
- 03:01
root of five thousand newton meters divided by forty five
- 03:04
kilograms which is about the same as one point five
- 03:06
meters times the square root of one Hundred over one
- 03:10
second squared giving us an answer of fifteen meters per
- 03:14
second So the answer Isi This is another case where
- 03:19
understanding the relationship between kinetic energy potential energy and mechanical
- 03:23
energy is the key to finding the right answer So
- 03:25
we have to make sure to study these forms of
- 03:27
energy And we know it's hard work studying so feel
- 03:30
free to take a snack break anytime you want Want 00:03:32.373 --> [endTime] some jelly beans will you
Related Videos
AP Physics 1: 2.5 Changes and Conservation Law. At what point(s) in this situation is energy lost in any form?
AP Physics 1: 1.4 Waves. Which of the following is technically true for Max as he stands at the edge of oblivion?
AP Physics 1: 1.4 Changes and Conservation Laws. Find the current across R2.
AP Physics 1: 2.4 Changes and Conservation Laws. Which of the following circuits should the students use?
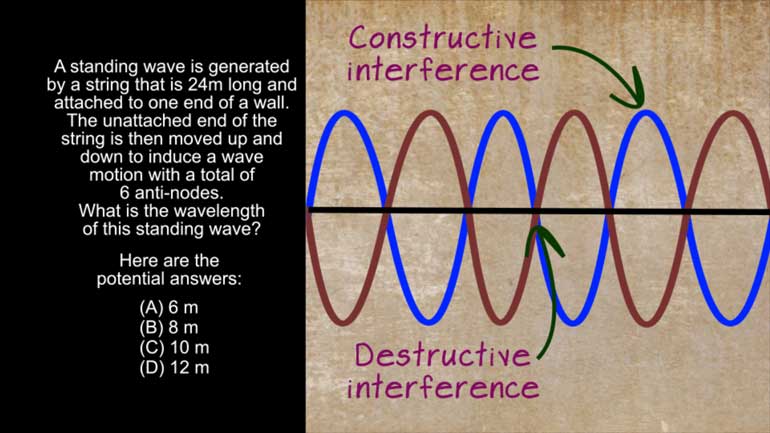
AP Physics 1: 1.5 Waves. What can possibly occur when the two waves reach each other?