Intermediate Value Theorem (IVT):
Let f be continuous on a closed interval [a, b]. Pick a y-value M, somewhere between f(a) and f(b). The Intermediate Value Theorem says there has to be some x-value, c, with a < c < b and f(c) = M. We'll use "IVT" interchangeably with Intermediate Value Theorem. It's just much easier to use an abbreviation.
Here's what's going on, in pictures. Start with a continuous function f on a closed interval [a, b]:
Mark on the y-axis where f(a) and f(b) are:
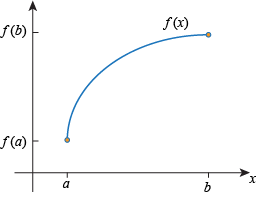
Pick any value of M strictly in between f(a) and f(b):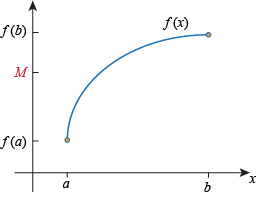
Draw a horizontal dashed line at height y = M. The IVT guarantees that this dashed line will hit the graph of f. In other words, the IVT guarantees the existence of some value c strictly in between a and b where the function value is M:
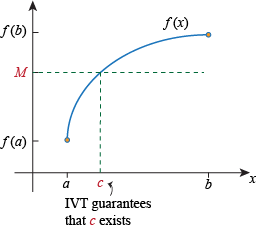
We've said a continuous function is one we can draw without lifting our pen from the paper. The IVT states this more precisely. If a continuous function starts at f(a) and ends at at f(b), then as x travels from a to b the function must hit every y value in between f(a) and f(b):
If a function on [a, b] skips a value, that function must be discontinuous:
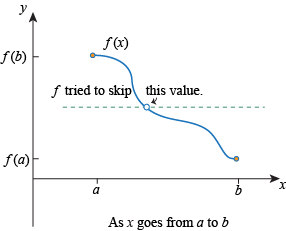
The statement of the theorem may be a little confusing, but with a few pictures this theorem shouldn't be much of a surprise. We're just making the whole notion of "drawing a continuous function without lifting our pencils" a little more formal.
Example 2
Can we use the IVT to conclude that  passes through y = 1 on  ? | |
No. We can't use the IVT in this case because the function f is discontinuous at x = 0. | |
Example 3
Can we use the IVT to conclude that  passes through y = 1 on (0, 1)? | |
No. This question doesn't even make sense. In order to use the IVT we need to know the function values at the endpoints of the interval, but f(0) is undefined.
| |
Example 4
Can we use the IVT to conclude that f(x) = x2 passes through y = 0 on (-1, 1)?
| |
No. Since f(a) = (-1) 2 = 1 and f(b) = (1) 2 = 1, 0 is not between f(a) and f(b). We cannot use the IVT in this situation. The function f does in fact pass through y = 0, but we know that by observation, not by using the IVT. Reminder: It doesn't matter whether we have f(a) < M < f(b) or f(b) < M < f(a), as long as M is between f(a) and f(b). | |
Exercise 1
- Can we use the IVT to conclude that f(x) = x3 + 2x + 1 passes through y = 0 on the interval (-2, 2)?
Answer
Yes. For starters, f is continuous on the closed interval [-2, 2]. We have a = -2 and b = 2, so
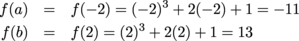
Since f(a) = -11 < 0 < 13 = f(b), the IVT says that there is some c with -2 < c < 2 and f(c) = 0.
Exercise 2
- Can we use the IVT to conclude that f(x) = ex passes through y = 0.1 on the interval (0, 1)?
Answer
No. With a = 0 and b = 1, f(a) = 1 and f(b) = e. The value 0.1 is not between 1 and e, so we can't use the IVT here.
Exercise 4
- Can we use the IVT to conclude that f(x) = tan(x) equals 0 for some c in (0, π)?
Answer
No. The function tan(x) is not continuous on [0, π] (it has a vertical asymptote on this interval), so we can't use the IVT.
Exercise 5
- Can we use the IVT to conclude that f(x) = x2 passes through 1 on the interval (-1, 1)?
Answer
No. The function f is indeed continuous on the closed interval [-1, 1], but with a = -1 and b = 1,
f(a) = f(b) = 1. The value 1 is not strictly in between 1 and 1 (if we wrote down 1 < 1 < 1 we would be lying), so the IVT won't fly here.
Exercise 6
- Draw a function that is continuous on [0, 1] with f(0) = 0, f(1) = 1, and f(0.5) = 20.
Answer
There are infinitely many right answers to this. Here's one of them:
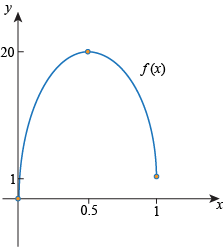
We could change the above problem to make f(0.5) equal anything we want.
Be Careful: We can never use the IVT to conclude that a function f fails to hit a value M.
Another thing to be aware of with the IVT is that it doesn't tell us where a function hits a value M, or how many times it does so. On its best day, the IVT can only guarantee we hit the value M at least once.
Exercise 7
- Suppose that f hits every value between y = 0 and y = 1 on the interval [0, 1]. Must f be continuous on that interval?
Answer
No. f could look like this, for example:
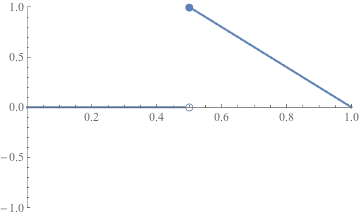
This function hits every value from 0 to 1 on the interval [0, 1], but f is discontinuous on this interval.
?
?
. With 
and 
, 
and f(b) = 1. Since f(a) = -1 < 0 < 1 = f(b),
the IVT says there is some c in between a and b (that is, 
), with 
. With 
and b = π, we have
and f(b) = sin(π) = 0. Since f(b) = 0 < 0.4 < 1 = f(a), the IVT says there is some c in 
with f(c) = 0.4.