Without a calculator, graph the polar function
r = 1 + sin θ
for
0 ≤ θ ≤ 2π.
Answer
Again, r is never negative because
r = 1 + sin θ
is always between 0 and 2.
Find the value of r at some nice angles.
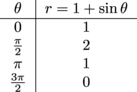
This gives us some points to start from.
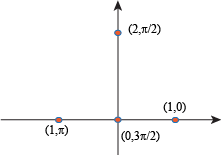
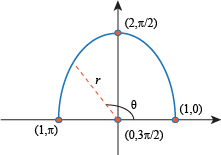
Now we need to figure out what's going on in between these points. Remember that r is never negative.
From θ = 0 to  , the value of r will move from 1 to 2.
, the value of r will move from 1 to 2.

From  to θ = π, the value of r will move from 2 to 1.
to θ = π, the value of r will move from 2 to 1.
From θ = π to  , the value of r will move from 1 to 0.
, the value of r will move from 1 to 0.
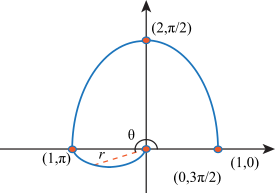
From  to θ = 2π, the value of r will move from 0 to 1.
to θ = 2π, the value of r will move from 0 to 1.
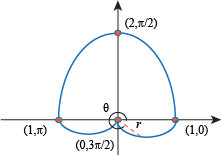
Again, we end with a heart shape that looks nothing like the graph
r = sin θ.
The moral is that adding constants does weird things to a polar graph.
 for 0 ≤ θ ≤ 4π.
for 0 ≤ θ ≤ 4π.


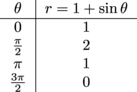

 , the value of r will move from 1 to 2.
, the value of r will move from 1 to 2.

 , the value of r will move from 1 to 0.
, the value of r will move from 1 to 0.
