Think you’ve got your head wrapped around Points, Vectors, and Functions? Put your knowledge to
the test. Good luck — the Stickman is counting on you!
Q. Which of the following statements is true?
The equation x2 = y2 describes y as a function of x.
The equation y2 = x2 describes x as a function of y.
The equation y = x2 describes y as a function of x.
The equation x2 = y describes x as a function of y.
Q. We say y = f(x) is a function of x if
there is only one possible y for each x.
there is only one possible x for each y.
both (A) and (B) hold.
none of the above.
Q. Which of the following functions is bounded above but not bounded below?
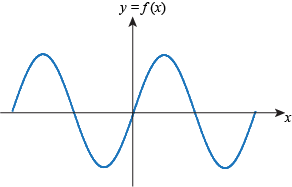
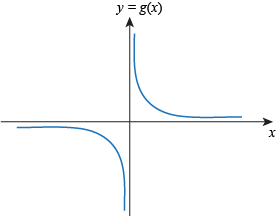
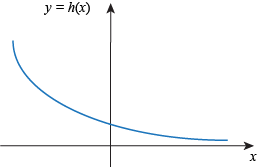
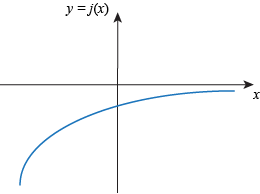
Q. We say a function f(x) defined on the whole real line is bounded below if
There is a real number K such that f(x) ≤ K for all real x.
There is a real number x such that f(x) ≤ K for all real K.
There is a real number K such that f(x) ≥ K for all real x.
There is a real number x such that f(x) ≥ K for all real K.
Q. Which of the following statements is FALSE?
If a function is strictly increasing, that function must also be non-decreasing.
If a function is non-decreasing, that function must also be strictly increasing.
It is possible for a function to be both non-decreasing and non-increasing.
It is possible for a function to be neither strictly increasing nor strictly decreasing.
Q. Which of the following graphs shows a function that is non-increasing but is not strictly decreasing?
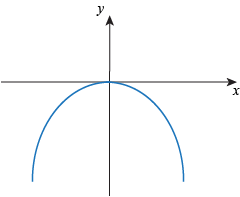
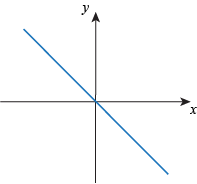
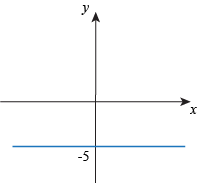
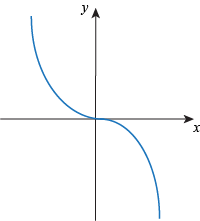
Q. Which of the following graphs shows an even function?
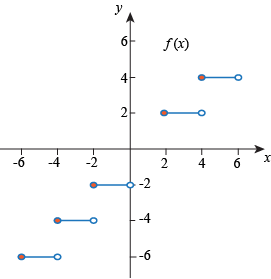
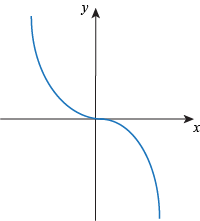
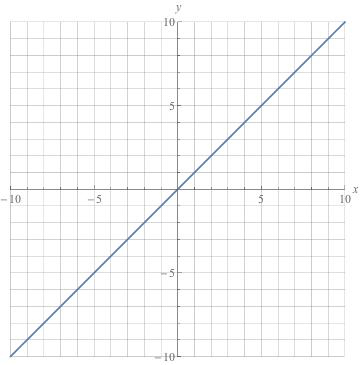
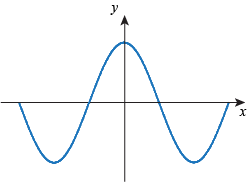
Q. Which of the following functions is odd?
f(x) = x2
f(x) = x + x2
f(x) = x + x
f(x) = x2 + x
Q. Which of the following statements is true?
A function must be either even or odd.
A function cannot be both even and odd.
It is possible for a function to be neither even nor odd.
If a function is not even, then that function must be odd.
Q. Which graph shows a function that is strictly decreasing, odd, and bounded both above and below?

A
B
C
D