Second Derivatives and Beyond Exercises

Answer

• Find dots.

The function f is undefined and has a vertical asymptote when x = 0. This function has no roots.

The derivative is

This is zero when x = 1. Since , we have a critical point at (1, e).

The second derivative is

Use the quadratic formula to see if x² – 2x + 2 has any roots.

We can't take the square root of a negative number so the answer is no.

f" is undefined at 0, so f has no inflection points.

• Find shapes.

We start with the numberline.

The function is positive when x is positive and negative when x is negative.

The derivative is negative when x < 1 and positive when x > 1.

Now for the sign of the second derivative.

Since the polynomial x² – 2x + 2 opens upwards and never hits the x-axis, it must always be positive. Since e^x and x⁴ are also positive, the only factor of f" that isn't always positive is x:

This means f" is negative when x is negative, and positive when x is positive.

Now we can find the shapes:

• Play connect-the-dots.

The final graph looks like this:

Answer

f (x) = x³ – 5x

• Find dots.

To find the roots, we factor the function:

f (x) = x(x² – 5)

The roots are x = 0 and . The root x = 0 is also the y-intercept.

The derivative of f is

f '(x) = 3x² – 5.

This is zero when

so these are our critical points. For the sake of graphing, The corresponding y values are

The second derivative is

f"(x) = 6x.

This is 0 when x = 0, so that's our inflection point.

We graph the dots, labeling their type. So long as it's written down somewhere what the coordinates of the critical points are, don't worry too much about trying to fit that label on the graph.

• Find shapes.

Here are the numberlines:

f (x) = x(x² – 5) is negative when x is negative and x² – 5 is positive, which occurs when . f is also negative when x is positive and (x² – 5) is negative, which occurs when . f is positive everywhere else.

f '(x) = 3x² – 5 is negative when and positive everywhere else.

f"(x) = 6x is negative when x is negative and positive when x is positive.

Now we can find the shapes:

• Play connect-the-dots.

Here's the graph:

Answer

f (x) = x²e^x

• Find dots.

The function f (x) is only zero when x = 0.

The derivative is

which is zero when x = 0 and when x = -2, so these are our critical points. When x = 0, we have y = 0 also.

f(-2) = 4e^-2

so the complete coordinates of the critical points are

(0, 0) and (-2, 4e^-2).

For the sake of graphing,

4e^-2 ≈ 0.54.

The second derivative (using the first definition of f ', not the factored version) is

This is zero when (x² + 4x + 2) is zero. We need the quadratic equation to solve this one:

We need to find the corresponding y-values.

• Find shapes.

Set up the numberline:

The function f is never negative.

The function f '(x) = xe^x(2 + x) is negative when exactly one of the quantities x and (2 + x) is negative, and positive otherwise. Therefore f ' is only negative when -2 < x < 0.

The function f "(x) = e^x(x² + 4x + 2) is negative when x is between the roots of the polynomial (x² + 4x + 2). That is, when

These are the shapes of f :

• Play connect-the-dots.

We play connect-the-dots, keeping in mind that f can't go below the x-axis:

Answer

• Find dots.

The function f is undefined when x = 1, and has a vertical asymptote there.

Before finding derivatives, rewrite the original function:

f (x) = 4(ln x)^-1

The derivative is

This is never undefined or 0 at a place where f is defined, so the function f has no critical points.

The second derivative is

This is undefined at the same places as f and f'. This is zero when

The corresponding y value of the inflection point is

For the sake of graphing,

e^-2 ≈ 0.135.

Here are the points:

• Find shapes.

We'll start with the numberlines.

The function f is negative when x < 1 and positive when x > 1.

The derivative

f'(x) = -4x^-1(ln x)^-2

is always negative, so f is always decreasing.

The second derivative is

The factors 4x^-2 and (ln x)^-2 are always positive, so the sign of f" is determined by the sign of the factor [1 + 2(ln x)^-1].

When x > 1, the quantity ln x is positive and so is [1 + 2(ln x)^-1].

When x < 1, we know there's a possible inflection point at e^-2 ≈ 0.135. We need to know what's going on with the sign of f" on the intervals

0 < x < e^-2

and

e^-2 < x < 1.

In order to not find too much of a headache, plug in some numbers and find the sign of [1 + 2(ln x)^-1]. Since e^-2  ≈ 0.135, we'll use x = 0.1 for the first interval and x = 0.5 for the second. When x = 0.1, we find

[1 + 2(ln 0.1)^-1] ≈ 0.131 > 0

so f " is greater than zero on the interval 0 < x <e^-2. When x = 0.5 we find [1 + 2 ln(0.5)^-1] ≈ -1.885 < 0 so f " is less than zero on the interval e^-2 < x < 1.This means f is concave up at the beginning of the graph, then concave down until the asymptote, then concave up again. Here are the shapes:

• Play connect-the-dots.

Here's the final graph:

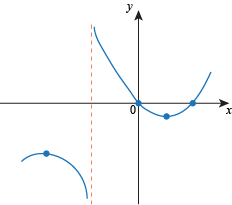
Answer

• Find dots.

The first thing to do is factor the numerator of f:

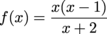
Now we can see that f is undefined with a vertical asymptote at x = -2, and has roots at x = 0 and x = 1.

The derivative of f is

This is zero when the numerator is zero, which occurs at (using the quadratic formula)

We have critical points at

The second derivative of f is

This is never 0, and is undefined at the same place f is undefined, so the function f has no inflection points.

Here are the dots:

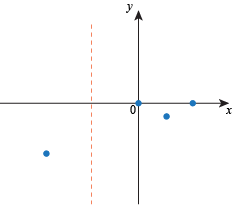
• Find shapes.

Here's the numberline:

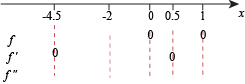
First, find the sign of the function .

When x < -2 all quantities x, (x – 1), and (x + 2) are negative, so f is negative.

When -2 < x < 0 the quantities in the numerator are both negative and the denominator is positive, so f is positive.

When 0 < x < 1 the quantity x – 1 is negative, while x and x + 2 are positive, so f is negative.

When 1 < x all quantities x, x – 1, and x + 2 are positive, so f is positive.

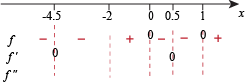
Next, the sign of .

The denominator is always positive, so we don't need to worry about that. Since f '(0) is negative, the derivative f ' is negative in between the two critical points. Plugging in some other numbers, we can see what the derivative is doing outside the critical points.

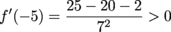
and

The derivative f' is positive outside the critical points.

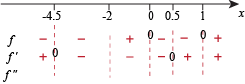
Finally, the sign of . This one is negative when x < -2 and positive when x > -2.

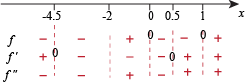
Using this, we find the shapes of f:

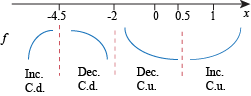
• Play connect-the-dots.

Here's the final picture.