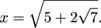Second Derivatives and Beyond Exercises

Answer

We use the quotient rule to find the derivative:

f '(x) is undefined only at x = -3, in which case f is also undefined so this is not a critical point. f '(x) is zero when

x² + 6x + 5 = 0.

Happily, this quadratic factors as

x² + 6x + 5 = (x + 5)(x + 1),

so f '(x) is zero at x = -5 and x = -1. Here's the numberline so far:

To use the second derivative test, we need to find the second derivative.

Now we evaluate the second derivative at each critical point. At x = -5 we find

which means f is concave down and so has a maximum at x = -5.

At x = -1 we find

which means f is concave up and so has a minimum at x = -1.

Thankfully, these are the same answers we found using the first derivative test.

Answer

The first derivative is

f '(x) = e^xcos x + e^xsin x = e^x(cos x + sin x).

This is never undefined. Since e^x is never 0, f ' is only 0 when

cos x + sin x = 0,

equivalently,

cos x = -sin x.

On the interval 0 < x < 2π, this only occurs at and , so these are our critical points. The second derivative is

f "(x) = e^x(-sin x) + e^xcos x + e^xcos x + e^xsin x = 2e^xcos x.

Now we need to find the sign of the second derivative at each critical point. Since 2e^x is always positive, the sign of f "(x) is the same as the sign of cos x.

Since is negative, we know

so f is concave down and has a maximum at . 

Since  is positive, we know 

so f is concave up and has a minimum at .

A graph of the function supports these answers:

Answer

The first derivative is

f '(x) = 3x² – 4x + 1

and the second derivative is

f "(x) = 6x – 4.

We use the first derivative to find the critical points. Happily, it factors:

The critical points are and x = 1. Now we find the (sign of) the second derivative at each critical point.

so f is concave down and has a maximum at x = ⅓.

f "(1) = 6(1) – 4 = 2 > 0

so f is concave up and has a minimum at x = 1.

Answer

The first derivative is

The only critical point is x = 1, since x = 0 isn't in the domain of f and e^x is never 0.The second derivative is

We could simplify this, but it's probably not worth it: all we need to do is plug in 1 for x and see what we find, so simplifying first would be a waste of time.

The function f is concave up at x = 1, and so there's a minimum there.

Answer

The derivative is

f '(x) = -sin x

and the second derivative is

f "(x) = -cos x.

On the interval specified, f ' is zero at

x = -π, 0, π

and never undefined, so these are all the critical points we need to worry about.Now we evaluate the second derivative at each critical point and see what we find.

f "(-π) = -cos(-π) = 1 > 0

so f is concave up and has a minimum at x = -π.

f "(0) = -cos 0 = -1 < 0

so f is concave down and has a maximum at x = 0.

f "(π) = -cos(π) = 1 > 0

so f is concave up and has a minimum at x = π.

Answer

f (x) = x⁴ – 32x

The first derivative is

f '(x) = 4x³ – 32.

This is zero when x = 2, so x = 2 is the single critical point of f. If we use the first derivative test, we need to evaluate f ' at two different values of x.

Since it's possible to take another derivative, we'll use the second derivative test. The second derivative is

f "(x) = 12x²

which is positive for any x ≠ 0. We didn't even need to evaluate f" at one value of x, which is nice. Since f " is positive at x = 2, the function f is concave up, and therefore has a minimum at x = 2.

Answer

f (x) = (x – 1)⁹

The first derivative is

f '(x) = 9(x – 1)⁸

which is zero when x = 1, so x = 1 is our only critical point. We can't use the second derivative test because

f "(x) = 72(x – 1)⁷

and therefore

f "(1) = 0.

This means we need to use the first derivative test. Take x = 0 for the point to the left, and x = 2 for the point to the right of our critical point.

f '(0) = 9(-1)⁸ > 0

and

f '(2) = 9(1)⁸ > 0

so f has neither a minimum nor a maximum at x = 1.

Answer

The first derivative is

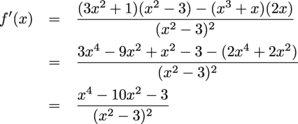
This one is nasty. We know that f ' is only undefined for x = , in which case f is also undefined, so we don't find any critical points that way. To find when f ' is zero we need to solve the equation

x⁴ – 10x² – 3 = 0.

We can use the quadratic formula to solve for x²:

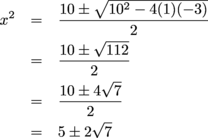
Since is negative and x² can't be negative, we know

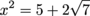
Therefore

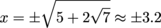
Now it's time to choose the first or second derivative test. If we use the second derivative test we need to find the second derivative, which requires the quotient rule again.

Instead, use the first derivative test. We have this numberline:

The numbers 0, ± 4 seem like nice ones to plug into the first derivative.

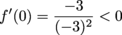
Since the first derivative contains only even powers of x, we know

f '(4) = f '(-4)

so we only need to evaluate one of these.

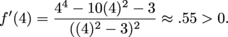
Now the numberline looks like this:

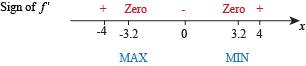
and we know that there is a maximum at

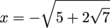
and a minimum at

Answer

f (x) = e^{x2 – 4x}

The first derivative is

f'(x) = (2x – 4)e^{x2 – 4x}

Since e^{x2  – 4x} is never zero or undefined, the only critical point occurs when 2x – 4 = 0, which is when x = 2. We could use the second derivative test, but that needs the product rule. Use the first derivative test. We know

e^{x2 – 4x} is always positive, so the sign of f ' is the same as the sign of 2x – 4. When x < 2 this is negative and when x > 2 this positive. We find this:

We conclude that f has a minimum at x = 2.

Answer

f (x) = x^2/3(1 – x²)

We can rewrite this function as

f (x) = x^2/3 – x^8/3.

Then the derivative is

This is undefined when x = 0, and zero when

We have critical points at x = 0 and . We can't use the second derivative test at x = 0 because f '(0) doesn't even exist. The first derivative test it is. Here's the numberline, and the values we need to plug into f':

We find

These next ones we'll do with a calculator. If you want to do them by scratch we recommend using x = ⅛ instead of x = 0.25, since ⅛ has a nice cube root. Remember, all we care about is whether we find positive or negative numbers.

Here's the numberline:

We have a min at x = 0, and maxima at x = ± ½.