Finding Shapes Examples

Find the shapes of the function f (x) = -4x³ + 3x + 2.

First we need to find the dots, because these dots will tell us the intervals we need to work with. Actually, for this part we only need to
find the x-values of the critical points and possible inflection points.

The derivative is f '(x) = -12x² + 3 which is zero when

We have critical points at .

The second derivative is f "(x) = -24x which is 0 when x = 0, so this is a possible inflection point.

Now that we've found the CPs and possible IPs, we make a numberline. The CPs and possible IPs divide the numberline up into intervals.

We need to know the signs of f ' and f " on each of these intervals. We draw dashed lines so we can keep the intervals straight:

The derivative is positive when

12x² < 3

which occurs when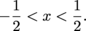

The derivative is negative otherwise. Fill this in on the numberline:

The second derivative is negative when x is positive, and positive when x is negative:

Now we can see what shape f should have on each interval: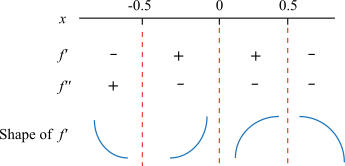

The numberlines in the graphing exercises will also include a numberline for the sign of the function f, because seeing where f is positive and negative is useful for drawing the graph correctly. However, you don't need to know the sign of f to determine the shape of f.