Think you’ve got your head wrapped around Second Derivatives and Beyond? Put your knowledge to
the test. Good luck — the Stickman is counting on you!
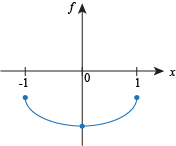
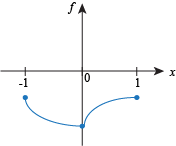
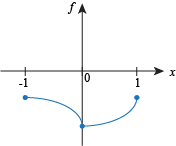
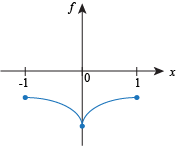
Q. Which of the following functions has neither a global maximum or a global minimum?
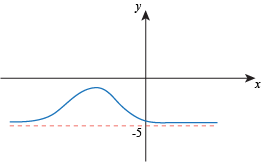
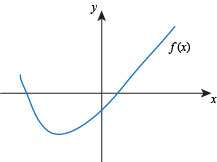
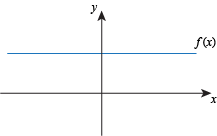
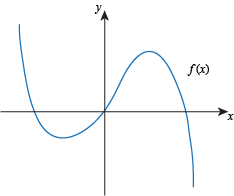
Q. A continuous function on an open interval
must have a global max and a global min.
cannot have a global max or a global min.
may or may not have a global max and/or a global min.
must have a global max if it has a global min.
Q. Which of the following statements about the function f (x) = 
is correct?
is correct? f has a global max and a global min on the interval [-1,1].
f has a global max but no global min on the interval [-1,1].
f has a global min but no global max on the interval [-1,1].
f has neither a global max nor a global min on the interval [-1,1].
Q. What is the global maximum of the function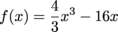 
on the interval [-3,3]?
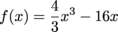on the interval [-3,3]? 
0
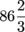
Q. Determine where the function f (x) = 4x4 + 2x is smallest on the interval [-2,2].
-2
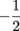
2
Q. Which of the following could be the start of a graph of the function f(x) = xex?
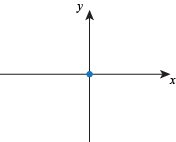
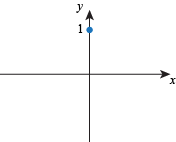
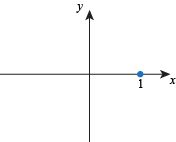
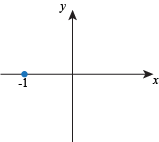
Q. Which of the following graphs could be a correct representation of all intercepts, critical points, and inflection points of the function f(x) = x2 – 3x – 4?
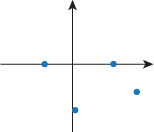
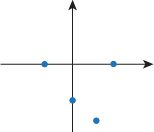
Q. If f ' is positive and f " is negative, what shape is the function f?
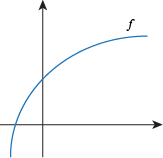
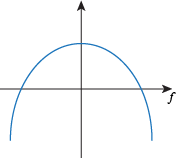
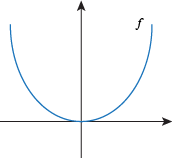
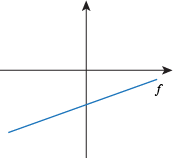
Q. The function f looks like this: 
Which of the following statements is true?
f ' is positive and f " is zero.
f ' is negative and f " is zero.
f ' and f " are both positive.
f ' and f " are both negative.
Q. The signs of the derivatives f ' and f " are as follows:
Use this information to fill in the graph of the function f :
