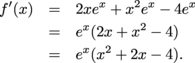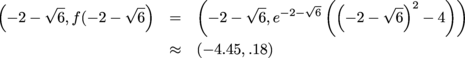There are three types of points to find on the function, and the great thing is that you already know how to find all of them.
- Intercepts: To find the y-intercept of a function, plug x = 0 into the function and see what we find. To find the x-intercepts, also known as roots, we set the function equal to zero and solve. Sometimes we'll also find vertical asymptotes in this step (find where f is undefined).
- Critical points: To find the critical points, set f '(x) = 0 (or undefined) and solve.
- Inflection points: To find the inflection points, set f "(x) = 0 (or undefined), solve, and check each solution to see if it's a real inflection point.
In summary, we're finding where f, f ', and f " are zero or undefined. These will mostly be dots, but there may be asymptotes or holes where f is undefined.
Here's the only thing you need to do that we didn't do earlier: after finding the x-value of a CP or IP, plug that x-value back into the original function f to find the corresponding y-value. In order to graph a point, we need to know both coordinates.
 , so this is our only critical point. In order to have a point to graph, we also need to know the y-value. We plug
, so this is our only critical point. In order to have a point to graph, we also need to know the y-value. We plug  back into the function:
back into the function:
 . For the sake of graphing, it's useful to know that
. For the sake of graphing, it's useful to know that