Ángulos de un polígono
Como ya adelantamos, los tres ángulos internos de un triángulo siempre suman 180°.
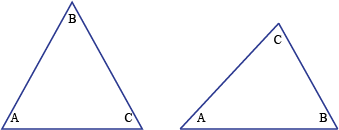
En cada caso ∠A + ∠B + ∠C = 180°.
Para encontrar los ángulos de cualquier polígono, todo lo que tenemos que hacer es dividirlo en triángulos. Para hacerlo, traza diagonales desde cualquier vértice hacia todos los demás vértices no adyacentes.
| Aquí tenemos un cuadrilátero. |  |
| Si trazamos diagonales desde un vértice, nos quedan dos triángulos. | |
| Cada triángulo tiene 180°, 2 × 180° = 360° |
| Pentágono – 5 lados |  | 3 triángulos × 180° = 540° |
| Hexágono – 6 lados |  | 4 triángulos × 180° = 720° |
| Heptágono – 7 lados |  | 5 triángulos × 180° = 900° |
| Octágono – 8 lados |  | 6 triángulos × 180° = 1080° |
¿Te das cuenta del patrón? Resulta ser que el número de triángulos formado al trazar diagonales desde uno de los vértices es el número de lados del polígono menos dos. Si le asignamos n al número de lados, podemos crear una fórmula para calcular el número de grados de cualquier polígono.
(n – 2) × 180°
Ángulos de un polígono. Ejemplo 1
¿Cuánto suman los ángulos internos de un dodecágono?
|
Ángulos de un polígono. Ejemplo 2
¿Cuánto mide cada ángulo en un nonágono regular?
|
Ángulos de un polígono. Ejemplo 3
Encuentra el ángulo que falta.
|
Ángulos de un polígono. Ejemplo 4
Encuentra Q.
|
Ángulos de un polígono. Ejemplo 5
Encuentra el ángulo que falta en el siguiente trapezoide isósceles.
|
Ángulos de un polígono. Ejercicio 1
¿Cuánto suman los ángulos internos de un decágono?
Ángulos de un polígono. Ejercicio 2
¿Cuánto mide cada ángulo de un hexágono regular?
Ángulos de un polígono. Ejercicio 3
Encuentra el ángulo que falta en el triángulo.
Ángulos de un polígono. Ejercicio 4
Encuentra el ángulo que falta en el triángulo.
Ángulos de un polígono. Ejercicio 5
Encuentra el ángulo que falta.
