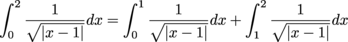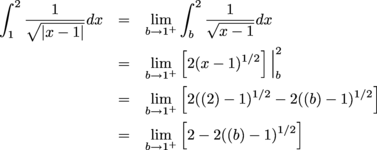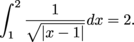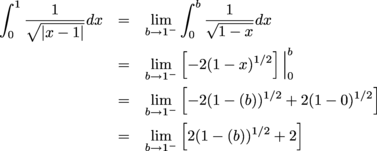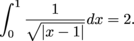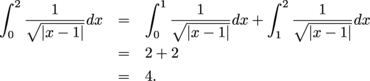Example 1
Determine whether the integral converges or diverges. If the integral converges, find its value.

Example 2
Determine whether the integral converges or diverges. If the integral converges, find its value.

Example 3
Determine whether the integral converges or diverges. If the integral converges, find its value.

Example 4
Determine whether the integral converges or diverges. If the integral converges, find its value.
 for p > 1
for p > 1
Example 5
Determine whether the integral converges or diverges. If the integral converges, find its value.
 for p < 1
for p < 1
Example 6
Determine whether each statement is true or false. Explain your answers.
If  does not exist, then
does not exist, then

must diverge.
Example 7
If  does not exist, then
does not exist, then

must converge.
Example 8
Determine whether the integral converges or diverges, and find its value if it converges.

Example 9
Determine whether the integral converges or diverges, and find its value if it converges.


 approaches ∞ as b approaches 0. That means the area of this region is infinite.
approaches ∞ as b approaches 0. That means the area of this region is infinite.
 .
.

 in another problem.
in another problem.





 is positive, which is reassuring since the area between
is positive, which is reassuring since the area between  and the x-axis on (0, 1] is all above the x-axis.
and the x-axis on (0, 1] is all above the x-axis. on the interval [-1,0). This graph is the graph of
on the interval [-1,0). This graph is the graph of  reflected over the y-axis.
Then
reflected over the y-axis.
Then  does not exist and
does not exist and 
 on the interval [-1,0), then
on the interval [-1,0), then  does not exist and
does not exist and 


 approaches ∞, which means e1/b approaches ∞ also. This integral diverges, which means the original integral diverges. We don't have to bother with the other integral.
approaches ∞, which means e1/b approaches ∞ also. This integral diverges, which means the original integral diverges. We don't have to bother with the other integral.