Example 1
Look at the picture below, which shows a region A within a region B.

If the area of region A is infinite, what does that tell us about the area of region B?
Example 2
Look at the picture below, which shows a region A within a region B.

If the area of region B is finite, what does that tell us about the area of region A?
Example 3
Look at the picture below, which shows a region A within a region B.

If the area of region A is finite, what does that tell us about the area of region B?
Example 4
Look at the picture below, which shows a region A within a region B.

If the area of region B is infinite, what does that tell us about the area of region A?
Example 5
From the graph below, determine if each integral converges, diverges, or if its behavior cannot be determined.

(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
Example 6
From the graph below, determine if each integral converges, diverges, or if its behavior cannot be determined.

(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
Example 7
From the graph below, determine if each integral converges, diverges, or if its behavior cannot be determined.

(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
Example 8
If 0 < f (x) and
 converges, does
converges, does
 converge or diverge?
converge or diverge?
Example 9
Use the graph to determine if  converges or diverges.
converges or diverges.

Example 10
Does  converge or diverge?
converge or diverge?

 , but since
, but since
 and
and





 and
and


 doesn't help, because
doesn't help, because



 is the same as the function
is the same as the function  . We know the integral of this function from 0 to 1 converges, and the integral of this function from 1 to ∞ diverges.
. We know the integral of this function from 0 to 1 converges, and the integral of this function from 1 to ∞ diverges. and
and



 that doesn't help us at all.
that doesn't help us at all.




 , we can't tell what
, we can't tell what
 and
and 



 on (0,1] and
on (0,1] and 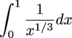
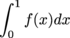
 on [1,∞) and
on [1,∞) and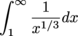
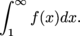
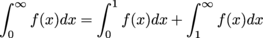
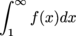
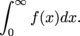
 on [0,1), but the integral
on [0,1), but the integral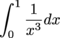
 on [0,1), but
on [0,1), but 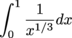
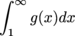
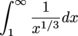
 on [1,∞).
on [1,∞).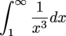
 on [1,∞).
on [1,∞).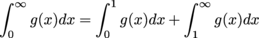





 , and
, and

