Example 1
A test contained the following question:

Laurie wrote down the following answer:
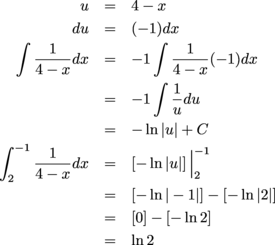
What did Laurie do wrong? What is the correct value of the integral?
Example 2
Evaluate the definite integral using Way 1(first integrate the indefinite integral, then use the FTC).

Example 3
Evaluate the definite integral using Way 1(first integrate the indefinite integral, then use the FTC).

Example 4
Evaluate the definite integral using Way 1(first integrate the indefinite integral, then use the FTC).

Example 5
Evaluate the definite integral using Way 1(first integrate the indefinite integral, then use the FTC).

Example 6
Evaluate the definite integral using Way 1(first integrate the indefinite integral, then use the FTC).

Example 7
A test contained the following question:

KT wrote down the following answer:

What did KT do wrong? What is the correct value of the integral?
Example 8
Evaluate the definite integral by substitution, using Way 2.

Example 9
Evaluate the definite integral by substitution, using Way 2.

Example 10
Evaluate the definite integral by substitution, using Way 2.

Example 11
Evaluate the definite integral by substitution, using Way 2.

Example 12
Evaluate the definite integral by substitution, using Way 2.









 .
.




 . So
. So






















 we have
we have







