Integration by partial fractions is a technique we can use to integrate rational functions when the degree of the numerator is less than the degree of the denominator. Here's the big picture:
- We start out with an integral whose integrand is a rational function, like
The degree of the numerator must be less than the degree of the denominator.
- We do some sneaky stuff to rewrite the original rational function as a sum of partial fractions:
- We integrate the partial fractions, whose antiderivatives all involve the natural log:
Be Careful: When x occurs in a denominator with a coefficient other than 1, you have to use integration by substitution.
.
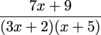
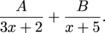
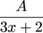
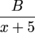
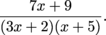
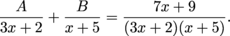
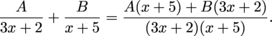
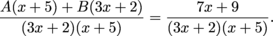
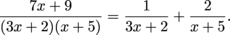
into partial fractions.
.
(because that's a little nicer than 
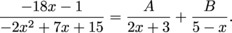
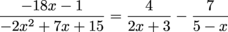
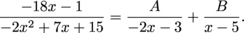
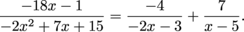
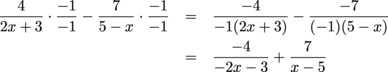
) and solve for A:
and solve for A:
