Find the first 5 partial sums of the alternating series
What do you notice about the partial sums?
Answer
The first 5 partial sums are
There are several things you could notice. Here are some of them:
The numbers seem to come in pairs, one negative and then one positive. We get-2, + 2, -4, + 4.
The partial sums alternate between positive and negative.
The partial sums go up, then down, then up.
Example 2
Play with the alternating series
(a) Find the first 5 partial sums of this series. Write them so that each partial sum has a denominator of 32.
(b) Plot the sequence of partial sums on this graph:
(c) What do you notice about the behavior of the partial sums?
(d) Do you think this series converges? Why or why not?
Answer
(a)
Writing all the partial sums with a denominator of 32, we get
(b) The graph looks like this:
(c) The partial sums go down, then up, then down, then up, while getting closer together. It looks like they're converging to something.
(d) We know that if the sequence of partial sums converges then the series converges. Since it looks like the sequence of partial sums is converging to something, we would guess that the series converges.
Example 3
For the series, can we use the AST to say the series converges? If not, why not?
Answer
This is an alternating series. The magnitudes of the terms are strictly decreasing:
The absolute values of the terms converge to zero:
Thus the AST says this series converges.
Example 4
For the series, can we use the AST to say the series converges? If not, why not?
Answer
This is an alternating series. The magnitudes of the terms are strictly decreasing:
The absolute values converge to zero:
Thus the AST says this series converges.
Example 5
For the series, can we use the AST to say the series converges? If not, why not?
Answer
This is not an alternating series. Since (2n + 1) is always odd, the quantity
is always negative. We can't use the AST here.
Example 6
For the series, can we use the AST to say the series converges? If not, why not?
Answer
This is an alternating series. Since
0.1 < 1
we get smaller numbers as we take higher powers. This gives us both conditions:
|an| = 0.1n > 0.1n + 1 = |an + 1|
The AST says this series converges.
Example 7
For the series, can we use the AST to say the series converges? If not, why not?
Answer
We can't use the AST here because the magnitudes of the terms don't converge to zero.
diverges.
Example 8
Consider the alternating series
which converges by the AST. Find the error for each of the partial sums
(a) S9
(b) S98
Answer
(a) Look at some partial sums:
The partial sums jump down, then up, with S9 being an up-jump.
To get to the next partial sum we jump down:
and in so doing, we overshoot the line:
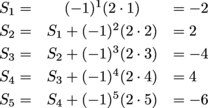
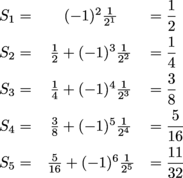
This means when we jumped down by , it was too much. The real sum of the series, L, must be within of S9.
In symbols,
(b) We have
Since the last term in this partial sum has a negative sign, we jumped down to get to S98. To get to S99 we jump up by , but this is too big a jump. The value we want is within of S98. In symbols,
, it was too much. The real sum of the series, L, must be within 
of S9.
, but this is too big a jump. The value we want is within 
of S98. In symbols,