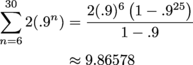Answer
1. This problem directly tells us everything we need to know. We're given a = 3 and r = 0.2. Since we're asked to find S7 we use n = 7.
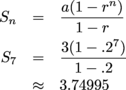
2. We're adding terms with denominators from 70 to 712. This means we're adding 13 terms together, so we must be finding S13. The first term is a = 2 and the ratio is 
.
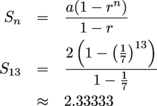
3. If we expand this series we get
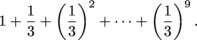
The first term is a = 1, the ratio is 
, and we're adding n = 10 terms (since the exponents on 
go from 0 to 9). Using the formula, we get
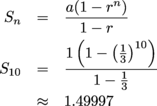
4. The first term is 
and the ratio is 
. If we rewrite the denominators, we can see that we're adding 8 terms, so n = 8:
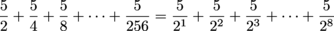
We get
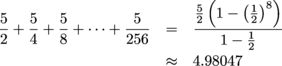
5. If we expand the sum we get
2(0.9)6 + ... + 2(0.9)30.
The first term is a = 2(0.9)6 and the ratio is r = 0.9. We're adding up terms with exponents from 6 to 30, so we're missing the exponents from 1 to 5.
This means we have
n = 30 – 5 = 25
terms. Applying the formula,
