Example 1
If the terms of a series approach zero, must the series converge? Justify or provide a counterexample.
Example 2
Does

converge or diverge?
Example 3
For the series, determine if it's okay to use the integral test. If so, use the integral test to determine whether the series converges or diverges.

Example 4
For the series, determine if it's okay to use the integral test. If so, use the integral test to determine whether the series converges or diverges.

Example 5
For the series, determine if it's okay to use the integral test. If so, use the integral test to determine whether the series converges or diverges.

Example 6
For the series, determine if it's okay to use the integral test. If so, use the integral test to determine whether the series converges or diverges.

Example 7
For the series, determine if it's okay to use the integral test. If so, use the integral test to determine whether the series converges or diverges.

 . This function is decreasing and non-negative on [1,∞), and the nth term of the series is f(n).
. This function is decreasing and non-negative on [1,∞), and the nth term of the series is f(n).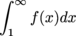
 is less than 1), the series must also diverge.
is less than 1), the series must also diverge.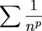







 as x goes to infinity:
as x goes to infinity:
