Diagramas de caja
Los diagramas de caja son una forma útil de graficar datos divididos en cuatro cuartiles, cada uno con igual cantidad de valores. El diagrama de caja no grafica frecuencia ni muestra las estadísticas individuales, pero en ellos podemos ver claramente dónde se encuentra la mitad de los datos. Es un buen diagrama para analizar la asimetría en los datos.
A continuación, te dejamos algunas palabras que debes tener en cuenta cuando graficas diagramas de caja:
- Q1 – Cuartil 1, la mediana de la mitad menor de los datos.
- Q2 – Cuartil 2, la mediana de todos los datos.
- Q3 – Cuartil 3, la mediana de la mitad mayor de los datos.
- IQR – Rango intercuartil, la diferencia entre Q3 y Q1.
- Valores extremos – Los valores más pequeños y los más grandes de los datos.
Comencemos haciendo un diagrama de caja de la puntuación en el examen de geometría:
90, 94, 53, 68, 79, 84, 87, 72, 70, 69, 65, 89, 85, 83, 72
Paso 1: ordena los datos de menor a mayor.
53 65 68 69 70 72 79 83 84 85 87 89 90 94
Paso 2: encuentra la mediana de los datos.
Llamado también cuartil 2 (Q2).
Paso 3: encuentra la mediana de los datos menores que Q2.
Este sería el cuartil menor (Q1).
Paso 4: encuentra la mediana de la data mayor que Q2.
Este sería el cuartil mayor (Q3).

Paso 5: encuentra los valores extremos.
Estos serían los valores más grandes y más pequeños.
Valores extremos = 53 y 94.
Paso 6: crea una recta real que contenga todos los datos.
Deja que se extienda un poco más allá de los valores extremos.

Paso 7: dibuja una caja de Q1 a Q3 divididas por una recta en Q2. Luego extiende los "bigotes" por cada lado de la caja hacia los valores extremos.
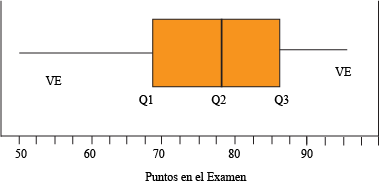
Esta gráfica está dividida en cuatro grupos distintos: el bigote menor, la mitad menor de la caja, la mitad mayor de la caja y el bigote mayor (el bigote mayor no se refiere a Jorge Negrete). Como en cada grupo hay una misma cantidad de datos, cada sección representa el 25% de los mismos.

A través de este diagrama vemos que el 50% de los estudiantes obtuvo entre 69 y 87 puntos, el 75% de los estudiantes obtuvo menos de 87 puntos y el 50% obtuvo más de 79. Si tu puntuación estuvo en el bigote mayor, siéntete orgulloso de ti mismo, ya que sacaste mejor nota que el 75% de tus compañeros. Si por el contrario, tu nota estuvo en el bigote menor, quizás tengas que estudiar un poco más (y ver las películas de Jorge Negrete después de estudiar).
Valores atípicos
Los valores atípicos son aquellos mucho más grandes o mucho más pequeños que el resto de los datos. Se representan con un punto en cualquier extremo del diagrama. En nuestro ejemplo no hubo ningún valor atípico; y aunque 53 parece ser mucho más pequeño que el resto, en realidad no fue lo suficientemente pequeño.
Para ser considerado un valor atípico, el valor debe ser:
- mayor que Q3 por, al menos, 1.5 veces el rango intercuartil (IQR), ó
- menor que Q1 por, al menos, 1.5 veces el IQR.
Los valores atípicos son aquellos que:
1.5(IQR) > Q3
1.5(IQR) < Q1
A continuación, te presentamos los resultados individuales finales de salto de esquí masculino de los Juegos Olímpicos de invierno.
| 283.6 | 269.4 | 262.2 | 261.1 | 246.7 |
| 245.5 | 239.2 | 233.7 | 230.3 | 227.9 |
| 226.4 | 225.5 | 224.1 | 223.6 | 222.3 |
| 221.4 | 217.8 | 217.2 | 216.9 | 211.6 |
| 211.4 | 208.5 | 204.9 | 202.7 | 202.4 |
| 200.5 | 198.5 | 182.4 | 111 |
Los cuartiles quedan así: Q1 sería 208.5, Q2 sería 222.3 y Q3 sería 236.45. La puntuación más baja (111) parece ser un valor atípico, ya que es mucho más pequeña que el resto de los datos. Sin embargo, no podemos estar seguros hasta que saquemos las cuentas.
Primero debemos calcular el IQR, que es Q3 – Q1. Luego lo multiplicamos por 1.5 para obtener el número que necesitamos para saber si hay algún valor atípico.
IQR = 236.45 – 208.50 = 27.95
1.5(IQR) = 1.5(27.95) = 41.93
208.5 – 41.93 = 166.57
Para que el número en cuestión (111) califique como un valor atípico, debe ser menor a 166.57, que es la diferencia entre Q1 (208.5) y 41.93.
¡Sí, es! Como 111 es menor a 166.57, entonces declaramos oficialmente a 111 como un valor atípico. Al hacer el diagrama de caja, representamos a 111 con un punto y extendemos el bigote menor solo hasta el siguiente valor menor (que sería 182.4).

Quizá deberíamos verificar que no haya ningún valor atípico hacia la mitad mayor de los datos.
236.45 + 41.93 = 278.38
Hay un valor cerca de 278.38, así que éste también es un valor atípico.
Diagrama de caja. Ejemplo 1
El siguiente diagrama representa la cantidad de dinero que Mateo se ganó en las últimas 18 semanas trabajando en la tienda de su papá. Crea un diagrama de caja y bigote con estos datos.
12|0 representa $120
La mediana (Q2) está entre 136 y 137. Es 136.5. El cuartil menor (Q1) es 130. El cuartil mayor (Q3) es 143. |






